Learning Objectives
In this article, the author has explained the following topics related to gas with laws examples.
- Gas laws
- Boyle’s law
- Charles’s law
- Avogadro’s law
Gas laws
Table of Contents
It is a fact that all the gases behave uniformly. When pressure and temperature are changed then the volume of gases is also changed. The gas laws describe the uniform behavior of gases.
The relationships between the volume of gases and the external conditions like temperature and pressure are called the gas laws.
Definition of gas laws
There are different gas laws presented by different scientists around the world.
Boyle’s law
Robert Boyle gave this law in 1662.
According to Boyle’s law
At constant temperature, the volume of a given mass of gas is inversely proportional to the pressure excreted on it.
Definition of Boyle’s law
Just suppose we have a gas, and if we apply pressure to this gas at constant temperature, then the volume of this gas will be inversely proportional to the pressure we applied.

The above equation 1 results into another statement of the Boyle’s law
At constant temperature, the product of pressure and volume of a given mass of a gas is always constant.
If the pressure of a given mass of gas is P1 and volume V1, then by changing pressure to P2, volume is changed into V2 such that
So P1V1=P2V2
Experimental verification of Boyle’s law
Consider a gas in a cylinder with a moveable piston at 25 °C. The cylinder is fitted with a manometer to read the pressure of the gas directly.
Let the initial volume of gas enclosed in cylinder is 1dm3 and pressure is 2 atm.
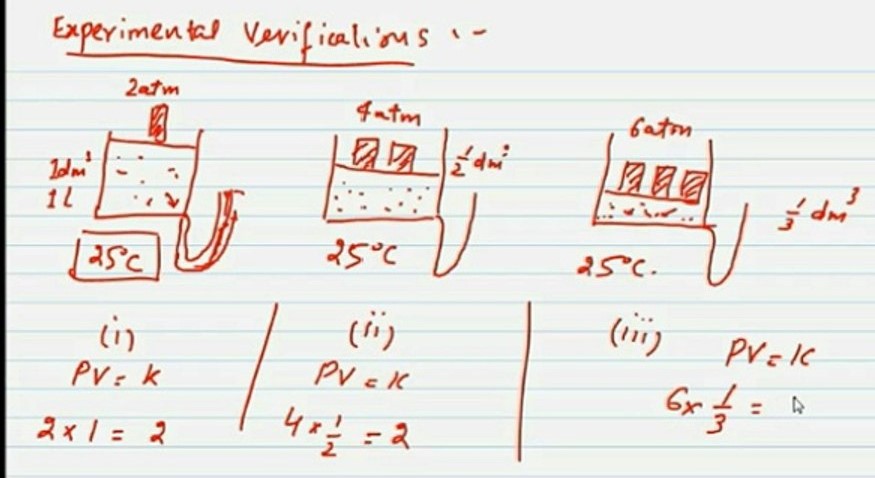
Now as Boyle’s law states
P1vi = 2 x 1=2 atm dm3 atm = k
When pressure is doubled on the gas, its volume becomes half.
Thus P = 4 atm and V = 1.2 dm3
Therefore, P2V2 = 4 x ½ = 2atm dm3 = k
Similarly, if pressure is tripled ( 6 atm) on the gas its volume is reduced to 1/3.
P3V3 = 6 x 1/3 = 2 atm dm3 = k
Since the product of P and V is always constant. Hence Boyle’s law is verified.
Example of Boyle’s law
A gas having a volume of 10 dm3 is enclosed in a vessel at 0 °C and the pressure is 2.5 atm. This gas is allowed to expand until the new pressure is 2 atm. What will be the new volume of this gas, if the temperature is maintained at 273 K?
Solution:

Isotherm (Graph between V and P)
The plot of the volume of a gas on the Y-axis and pressure on the X-axis at constant temperature ( 0°C) gives a curve called isotherm.
Definition of isotherm
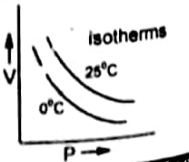
If this graph is plotted at higher temperature such as 25 °C then the curve goes away from both axis because at high temperature the volume of gases is increased.
Similarly, if we plot the curve at further higher temperature then the curve further goes away from the two axes.
Graph between P and 1/V
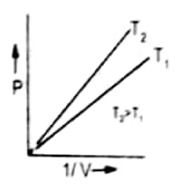
The plot of pressure P on Y-axis against inverse volume ( 1/V) of a gas on X-axis results into a straight line. The reason behind this is that increase in pressure decreases the volume hence inverse of volume increases. Therefore, P is directly proportional to 1/V.
At the higher temperature straight line becomes closer to Y-axis. It is increased at higher temperature the volume of a gas is increased, therefore, 1/V is decreased.
The straight line passes through the origin because when the pressure is close to zero then volume is so high that 1/V is very close to zero.
Graph between PV and P
A plot of P on the X-axis against PV on the Y-axis will give a straight line parallel to X-axis. The straight line shows that K constant quantity.
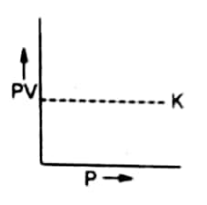
At higher temperatures, the volume of gas is increased. But the new value of PV also remains constant. Therefore, a straight line parallel to X-axis is again obtained at higher temperatures.
This straight-line helps us to understand the non-ideal behavior of gases.
Boyel’s law is only applicable to the ideal gases.
Charles’s law
Charles was a French scientist who gave this law in 1787.
According to the Charles’s law
At constant pressure, the volume of a fixed mass of gas is directly proportional to the absolute temperature.
Definition of Charles’s law
Mathematically it can be represented as
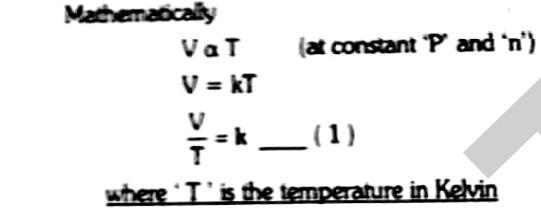
Where T is the temperature in Kelvin
It can also be represented as
V1/T1=V2/T2=K
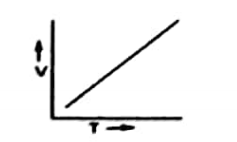
Equation # 1 shows that
At constant pressure, the V of a given mass of of gas and T will be a straight line. It is because V is directly proportional to the absolute temperature.
Experimental verification of Charles’s law
If we consider a gas which is enclosed in a cylinder fitted with a moveable piston. At temperaute T1 the volume of gas is V1.
If we increase the temperature to T2, then the volume of gas is increased to V2. The pressure on the piston is kept constant.
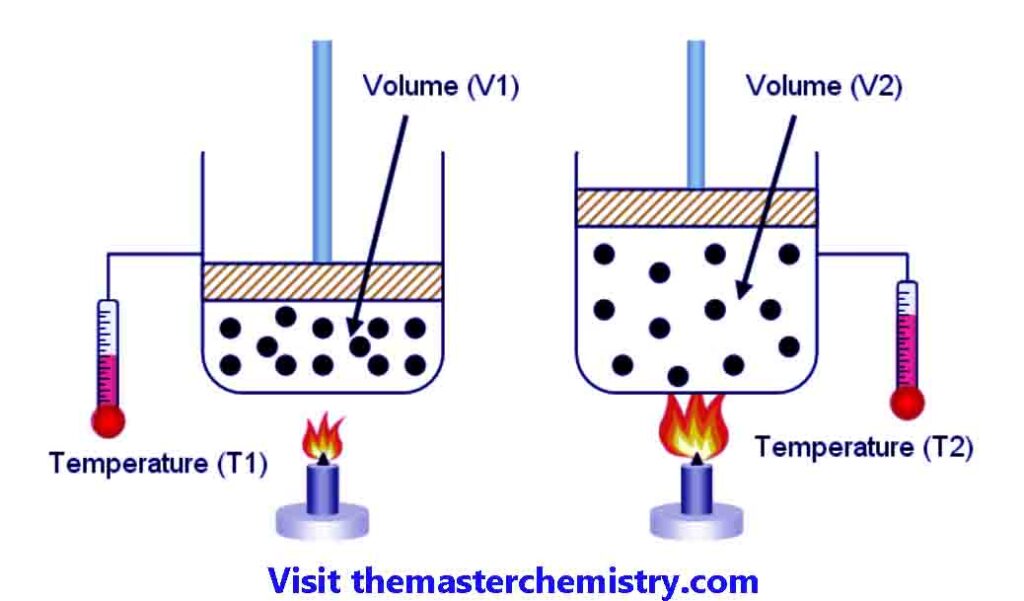
It is observed that ratio between colume of a given mass of gas and temperature remains constant at constant pressure.
For example V1T1=V2/T2=k
Verification of temperature scale for Charles’s law
He mathematical form of Charles’s law is V/T = k
This equation only holds if temperature is on Kelvin scale.
To better understand this have a look at the table below.
Consder the following data for a gas when the temperature is on Kelvin scale
| V (dm3) | 1092 | 846 | 746 |
| T (K) | 546 | 423 | 373 |
| VT (dm3K-1) | 2 | 2 | 2 |
As we can see that V/T is always constant.
However, if temperature is taken on Celcius scale then the above relation is not satisfied. For example consider the following data for above gas when the temperature is on centigrade scale
| V (dm3) | 1092 | 846 | 746 |
| T (°C) | 273 | 150 | 100 |
| VT (dm3 °C | 4 | 5.64 | 7.46 |
Therefore, value of V/T does not remains constant.
Thus we can say that Charles’s law is only obeyed if temperature is on Kelvin scale.
250 cm3 of hydrogen is cooled from 127 °C to -27°C by maintaining the pressure constant. Calculate the new volume of the gas at low temperature.
Solution
V1= 250 cm3 V2=?

Avogadro’s law
It states
Equal volume of all the gases (ideal) at the same temperature and pressure contain equal number of molecules or moles.
Definition of Avogadro’s law
So, number of moles of a gas is directly proportional to its volume.
i.e; V α n
It shows that same number of moles of all gases occupies same volume at same temperature and pressure. The volume occupied by one mole of any gas at STP is called molar volume and is equal to 22.414 dm3.
STP stands for Standard Temperature and pressure
One mole of any gas contains constant number of molecules. This number is called Avogadro’s number. Its value is 6.02 x 10 23.
For example:
1 mole of O2 = 32 g O2 = 22.414 dm3 at STP = 6.02 x 10 23 molecules of O2
1 mole of H2 = 2.016 g H2 = 22.414 dm3 at STP = 6.02 x 10 23 molecules of H2
So,
1 mole of O2 and H2 occupies same volume at STP although O2 is 16 times heavier than H2.
The reason is that molecules in gases are widely separated from one another and have large empty spaces. The distance between two molecules is approximately 300 times the diameter of the molecule.
Therefore, size and masses of gas molecules do not affect their volume. Hence equal moles of all gases occupy same volume at STP.
Facts about Avogadro’s law
One dm3 of every gas at STP will have molecules = 6.02×1023/22.424 = 2.68 x 10 23 molecules.
If temperature and pressure are changed equally for all gases, each gas will have same 2.68×1023 molecules.
One dm3 of H2 at STP weighs 0.0899 g. Since (2.016/22.424 =0.0899g) and one dm3 of O2 at STP weighs 1.4384 g since ( 32/22.414 = 1.4384g) but they contain equal number of molecules ( i.e. 2.68 x 1023).