Distribution Law In Chemistry-Definition, Explanation, And Applications

Learning objectives

In this article, the author has explained the following topics

Distribution law
Distribution coefficient
Applications of distribution law
limitations of distribution law

Distribution law or partition law

Table of Contents

At constant temperature, a solute distributes itself between two immiscible liquids in a constant ratio of concentration, independent of the amount of solute added.
Definition of distribution law

Two important techniques are totally based on the distribution law.

Solvent extraction
Partition chromatography

Distribution coefficient

At constant temperature, the ratio of the concentration of a substance in two immiscible liquids, present in equilibrium with each other, is called distribution co-efficient.
Definition of distribution coefficient

It is represented by K

If we talk about its mathematical expression then

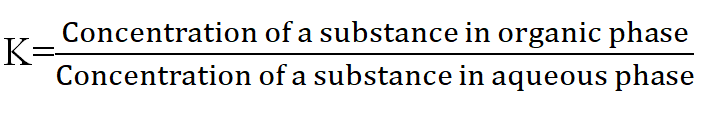
Mathematical expression of distribution coefficient

In above equation the organic phase may be a organic solvent such as CCl₄ and aqueous phase is water.

Nernst’s Distribution Law

In 1891 Nernst studied the distribution of several solutes between different appropriate pairs of solvents. He gave a generalization which governs the distribution of a solute between two non-miscible solvents.

This is called Nernst’s distribution law.

If C1 denotes the concentration of the solute in solvent A and C₂ the concentration in solvent B, Nernst’s distribution law can be expressed as:

C₁/C₂ = Kd

The constant Kd or simple K is called the distribution coefficient or partition coefficient or distribution ratio.

Examples of distribution law or partition law

Distribution of iodine between CCl₄ and water containing KI

Consider the distribution of I₂ between two immiscible liquids, CCl₄ and water in the presence of Potassium iodide KI.

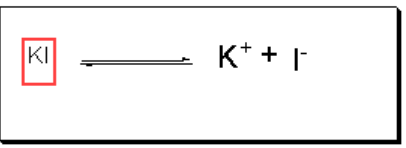
Iodine is insoluble in water while KI is added into water.

In water, KI ionizes into ions

Iodine combines with iodide ion to form tri-iodide ion in a reversible reaction.

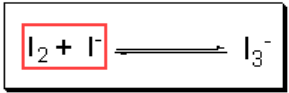
Thus iodine dissolves as I₃^– ion in water that is aqueous phase

Now if we add CCl₄ to an aqueous solution that contains tri-iodide ion. As iodine is more soluble in CCl₄ than in water therefore, it moves from aqueous layer to the CCl₄ layer that is organic layer.

As a result, the brown color of tri-iodide ion in the aqueous layer fades while the purple color of free iodine appears in CCl₄ layer.

This system of CCl₄ and H₂O is shaken to further increase the area of contact between the two layers. By doing so more and more iodine moves from the aqueous layer to the organic layer.

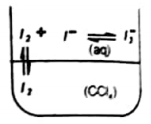
After repeating this process for some time, equilibrium is established between the two layers. At this point, the rate of movement of I₂ from H₂O to CCl₄ becomes equal to the rate of movement of I₂ from CCl₄ to H₂O.

Hence at equilibrium the ration of concentration of I₂ in both layers will be constant at constant temperature. This constant is called distribution co-efficient and it is denoted by K.

Distribution co-efficient is represented as

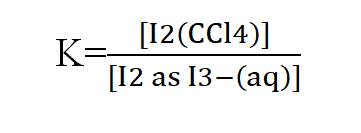
equation for Distribution of coefficient

Solved example 2:

A solid X is added to a mixture of benzene and water. After shaking well and allowing to stand, 10 ml of the benzene later was found to contain 0.13 g of X and 100 ml of water layer contained 0.22 g of X. Calculate the value of distribution coefficient.

Solution

Concentration of X in Benzene (C_b)= 0.13/10 = 0.013 g ml^-1

Concentration of X in water (C_w)= 0.22/100 = 0.0022 g ml^-1

According to distribution law

C_b/C_w = 0.013/0.0022 = 5.9

Solved example 2

In the distribution of succinic acid between ether and water at 15 degree centigrade, 20 ml of the ethereal layer contains 0.092 g of the acid. Find out the weight of the acid present in 50 ml of the aqueous solution in the equilibrium with it if the distribution coefficient for succinic acid between water and ether is 5.2.

Solution

Let the weight of succinic acid in aqueous layer be X g.

Concentration in aqueous layer = X/50 g ml^-1

Concentration in ethereal layer = 0.092/20 g ml^-1

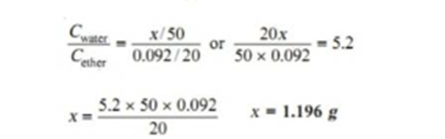
Solubilities and distribution law

When a solute is shaken with two non-miscible solvents at equilibrium both the solvents are saturated with the solute. Since the solubility also represents concentration we can write the distribution law as:

C₁/C₂=S₁/S₂=K_d

Where S1 and S2 are the solubilities of the solute in the two solvents.

Hence knowing the value of the distribution coefficient (K_d) and the solubility of the solute in one of the solvents the solubility of solute in the second solvent can be calculated.

Solved Problem

At 25 degree centigrade an aqueous solution of iodine containing 0.0516 g litre^-1 is in equilibrium with a carbon tetrachloride solution containing 4.412 g litre^-1. Find the solubility of iodine in carbon tetrachloride.

Solution

To find the value of Kd

Concentration of Iodine in water= 0.0573 litre^-1

Concentration of iodine in CCl₄= 4.412 litre^-1

The value of distribution coefficient is

C_ccl4/C_H2O= 4.412/0.0516= 85.5

Calculation of Solubility S

Applying the distribution law

Applications of distribution law or partition law

This law is helpful in many ways in industrial chemistry and physics.

It is much helpful in the separation and purification of substances from mixtures such as solvent extraction.
It is useful to determine the extent of hydrolysis
It also helps in the confirmation of the formula of the complexes such as CuSO₄.4NH₃
It is used to find the equilibrium constant for the equilibrium
It is used to determine the solubility of the different solutes in a solvent
It is used for solvent removal purposes
It is also helpful in the separation of high act liquid chromatography
It is used to conserve the emulsions and creams
It helps in the formation of the solubilized structure
Used to determine the solubility of the different drugs in specific solvents

Limitations of distribution or partition law

Although it is very useful law, but also have some limitations:

It is not functional in variable temperature condition
It does not describe the process of dissociation or association in different molecular state
The concentrations of the solute can only be noted when the equilibrium is established.
The concentration of the solute in the two solvents is low. This law does not hold when the concentrations are high.
The two solvents are non-miscible or only slightly soluble in each other. The extent of mutual solubility of the solvents remains unaltered by the addition of solute to them.

Let others know about this